Standardabweichung: Was sie ist, wozu sie dient und wie man sie berechnet

Die Standardabweichung ist eines der wichtigsten statistischen Maße bei der Berechnung einer Forschungsstichprobe und auch ein Risikomaß, das von Analysten, Portfoliomanagern und Beratern verwendet wird.

In diesem Artikel wird beschrieben, was die Standardabweichung ist, wofür sie verwendet wird und wie man sie Schritt für Schritt erhält.

Was ist die Standardabweichung?

Die Standardabweichung ist ein Maß für die Streuung oder Variabilität in der deskriptiven Statistik. Sie wird verwendet, um die Variation oder Streuung zu berechnen, um die einzelne Datenpunkte vom Mittelwert abweichen.

Eine geringe Abweichung zeigt an, dass die Datenpunkte sehr nahe am Mittelwert liegen, während eine hohe Abweichung zeigt, dass die Daten über einen größeren Wertebereich gestreut sind.

Im Marketing kann die Abweichung dazu beitragen, große Schwankungen bei Kosten oder Umsätzen zu berücksichtigen.

Die Standardabweichung hilft auch bei der Bestimmung der Streuung der Preise von Vermögenswerten von ihrem Durchschnittspreis und der Volatilität auf dem Markt.

Finden Sie auch heraus, was die mittlere Abweichung ist.

Beispielformel für die Standardabweichung

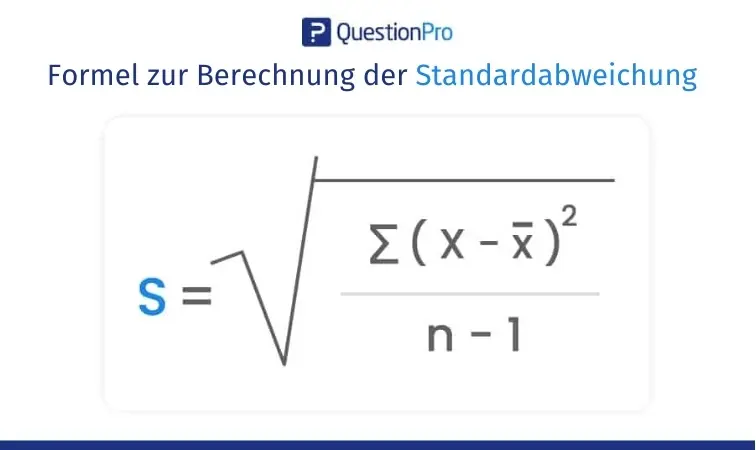
Die Standardabweichung ist eine Schlüsselkomponente bei der Berechnung des Umfangs der Untersuchungsstichprobe. Die Formel zu ihrer Berechnung lautet wie folgt:

* S = Standardabweichung.

* ∑ = Summe von.

* X = Jeder Wert.

* x̅ = Arithmetisches Mittel.

Wie berechnet man die Standardabweichung einer Stichprobe?

Um die Standardabweichung einer Stichprobe zu berechnen, führen Sie einfach die folgenden Schritte aus:

• Berechnen Sie den Mittelwert aller Datenpunkte. Der Mittelwert wird berechnet, indem alle Datenpunkte addiert und durch die Anzahl der Datenpunkte geteilt werden.
• Berechnen Sie die Varianz jedes Datenpunktes, indem Sie das Maß des Mittelwertes vom Wert des Datenpunktes abziehen.
• Quadrieren Sie die in Schritt 2 erhaltene Varianz jedes Datenpunktes.
• Addieren Sie die in Schritt 3 erhaltenen Werte der quadrierten Varianz.
• Teilen Sie die Summe der in Schritt 4 erhaltenen quadrierten Varianzwerte durch die Anzahl der Datenpunkte im Datensatz minus 1.
• Ziehen Sie die Quadratwurzel aus dem Quotienten des in Schritt 5 erhaltenen Ergebnisses.

Die Bedeutung der Standardabweichung

Die Standardabweichung ist ein wichtiger Faktor für die statistische Analyse. Einige Gründe dafür sind:

Standardabweichung schließt alle Beobachtungen ein.

Ein Vorteil der Abweichung ist, dass jeder Datenpunkt in die Analyse einbezogen wird. Andere Abweichungsmaße, wie z. B. die Spanne, messen nur die am weitesten auseinander liegenden Punkte, ohne die Punkte dazwischen zu berücksichtigen. Daher wird die Standardabweichung oft als robusteres und genaueres Maß im Vergleich zu anderen Beobachtungen angesehen.

Kann in Kombination verwendet werden

Die Standardabweichung zweier Datensätze kann mithilfe einer speziellen Formel für die kombinierte Abweichung kombiniert werden. Ähnliche Formeln gibt es für andere Streuungsmaße in der Statistik nicht. Darüber hinaus kann die Standardabweichung im Gegensatz zu anderen Beobachtungsmaßen in anderen algebraischen Berechnungen verwendet werden.

Mit ihr kann man feststellen, ob eine Menge ungleich verteilt ist.

Die Standardabweichung ist besonders nützlich, wenn Sie wissen wollen, inwieweit Ihr Datensatz ungleichmäßig verteilt ist. Sie gibt nicht nur Aufschluss über die Streuung der Daten, sondern auch über ihre ungleiche Verteilung.

Mit der Standardabweichung können Sie mathematische und statistische Analysen durchführen.

Der Wert der Standardabweichung ist immer fest und gut definiert, so dass sowohl mathematische als auch statistische Analysen durchgeführt werden können.

Sie ermöglicht es, die Volatilität einer Investition zu bestimmen

Die Volatilität einer Anlage lässt sich anhand der Anzahl der Datenpunkte bestimmen, die vom Mittelwert abweichen. Je mehr Datenpunkte vom Mittelwert abweichen, desto volatiler ist die Anlage.

     |   Erfahren Sie mehr über den Mittelwert, Median und Modus.

4 Anwendungsbereiche der Standardabweichung

Einige häufige Verwendungszwecke der Abweichung sind:

1. Messung des Anlagerisikos

Viele Wertpapierfirmen verwenden die Standardabweichung, um herauszufinden, wie stark die Wertentwicklung des Fonds von der normalen erwarteten Rendite abweicht. Wie leicht zu verstehen ist, kann diese Statistik den Endkunden und Anlegern mitgeteilt werden.

Auf diese Weise ermöglicht die Abweichung eine Bewertung der Volatilität von Wertpapieren auf dem Markt und eine Vorhersage künftiger Wertentwicklungstrends.

2. Besseres Verständnis von Datensätzen

Die Standardabweichung wird verwendet, um die Streuung von Werten in einem Datensatz zu messen. Privatpersonen und Unternehmen verwenden die Standardabweichung ständig in verschiedenen Bereichen, um Datensätze besser zu verstehen.

3. Verstehen Sie die Anzeigenleistung.

Vermarkter berechnen häufig die Standardabweichung der mit jeder Anzeige erzielten Einnahmen, um zu sehen, welche Schwankungen bei den Einnahmen für eine bestimmte Anzeige zu erwarten sind.

In diesem Bereich können Sie auch die Varianz der Anzahl der von Mitbewerbern genutzten Anzeigen berechnen, um zu verstehen, ob die Mitbewerber in einem bestimmten Zeitraum mehr oder weniger Anzeigen als normal nutzen.

4. Einsatz der Standardabweichung im Personalwesen

Zu den Aufgaben eines Personalleiters gehört es, die Standardabweichung der Gehälter in einem bestimmten Bereich zu berechnen, um zu wissen, welche Art von Gehaltsabweichung er neuen Mitarbeitern anbieten soll.

Fazit

Nun, da Sie alle Grundlagen über die Standardabweichung kennen, laden wir Sie ein, mehr über die Verwendung dieser und anderer Forschungsmaße und -techniken auf praktische Weise in unserem Ebook Advanced Research Methodik zu erfahren.

Vergessen Sie nicht, dass es völlig kostenlos ist, ebenso wie unser Stichprobenrechner, der Ihnen hilft, die ideale Grundgesamtheit für Ihre Studien zu finden, und natürlich unsere Online-Umfrageplattform Erstellen Sie jetzt Ihr Konto!

1:1 Live Online-Präsentation:
QUESTIONPRO MARKTFORSCHUNGS-SOFTWARE

Vereinbaren Sie einen individuellen Termin und entdecken Sie unsere Marktforschungs-Software.

Software für Marktforschung und Experience Management jetzt 10 Tage kostenlos testen!

Sie haben Fragen zum Inhalt dieses Blogs? Kontaktieren Sie uns ganz einfach über das Kontaktformular. Wir freuen uns auf den Dialog mit Ihnen! Testen Sie zudem QuestionPro 10 Tage kostenlos und ohne Risiko in aller Ruhe und Tiefe!

DIESEN ARTIKEL TEILEN

STICHWÖRTER DIESES BLOG-BEITRAGS

Standardabweichung | Formel | Marktforschung